Générateurs de nombres aléatoires
TP2 - Registres à décalage à rétroaction linéaire (LFSR)
TP2 - Registres à décalage à rétroaction linéaire (LFSR)
Le registre à décalage à rétroaction linéaire¶
Considérons le LFSR dont le polynôme de rétroaction est défini par : $$ f(X) = 1 + X^3 + X^5 + X^8 $$
Notons $\big(b_n\big)_{n\in\mathbb N}$ la suite générée par ce LFSR c'est à dire la suite récurrente binaire définie par : $$ \left\{\begin{array}{l} b_0, b_1, \dots, b_7 \in \{0, 1\}\\ \forall n\geq 8,\ b_{n} = b_{n-3} \oplus b_{n-5} \oplus b_{n-8} \end{array}\right.$$
On peut représenter ce LFSR de la manière suivante :
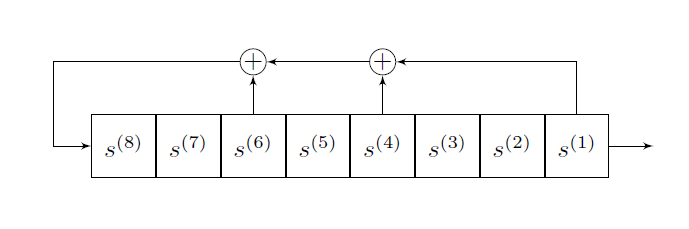
Remarquons qu'il s'agit, en fait, du GMR d'ordre 8 défini par :
- $S = \{0, 1\}^8$
- $f(\textbf{s}) = f\Big(s^{(1)},\ \dots\ ,\ s^{(8)}\Big) = \Big(s^{(2)},\ \dots\ ,\ s^{(8)},\ s^{(1)} + \ s^{(4)}\ + s^{(6)} \mod 2\Big)$
Ou encore du générateur digital défini par :
- $S = \{0, 1\}^8$
- $f(\textbf{s}) = A\textbf{s} \mod 2$ où $A$ désigne la matrice carrée $\left(\begin{array}{cccccccc} 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \\ 1 & 0 & 0 & 1 & 0 & 1 & 0 & 0 \\ \end{array}\right)$
Question 1 :
- Programmer une fonction monRegistre$(lst\_pos)$ qui change l'état du registre $reg$ (variable globale) et retourne son nouvel état : $\big[ reg[1],\ \dots,\ reg[7],\ a_0 reg[0] + \dots + a_7 reg[7] \mod 2\big]$ avec $a_k = 1$ si et seulement si $k$ appartient à $lst\_pos$
- Générer les registres jusqu'à la première répétition, en initialisant les 8 bits avec l'horloge de l'ordinateur, puis préciser la période
Le paramètre $lst\_pos$, ici égal à [0, 3, 5], permet de "généraliser" la fonction pour la réutiliser plus loin
# Réponse
A partir d'un état $\Big(s^{(1)},\ \dots\ ,s^{(8)}\Big)$ du registre, on peut générer un réel entre 0 et 1 (avec une précision de $2^{-8}$) défini par : $$u = \displaystyle\sum_{i=1}^8 s^{(i)}2^{-i} \quad (*)$$
Il s'agit, en fait, de la formule $g(\textbf{s}) = \displaystyle\sum_{i=1}^w \Big((B\textbf{s})_i \mod 2\Big)2^{-i}$ avec $B = I_8$.
En prenant $B = \left(\begin{array}{cccccccc} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0\\ \end{array}\right)$, on obtient toujours un réel entre 0 et 1 mais seulement avec une précision de $2^{-4}$ :
$$u = \displaystyle\sum_{i=1}^4 s^{(i)}2^{-i}$$Question 2 :
- Programmer une fonction regToReel$(reg)$ qui transforme un registre $reg$ de longueur 8 en un réel suivant la formule (*)
- Générer les réels jusqu'à la première répétition, en initialisant les 8 bits avec l'horloge de l'ordinateur
# Réponse
Question 3 :
- Programmer une fonction monLFSR_bit_N$(lst\_pos, g, N)$ qui retourne la liste des $N$ bits $b_0,\ \dots\ ,\ b_{N-1}$ générés à partir de la graine $g = (b_0,\ \dots\ ,\ b_{7})$
- Tester la fonction pour retrouver, au passage, le résultat de la question 1
# Réponse
Question 4 :
- Programmer une fonction monLFSR_reel_N$(lst\_pos, g, N)$ qui retourne la liste des $N$ réels $u_0,\ \dots\ ,\ u_{N-1}$ générés à partir de la graine $g = (b_0,\ \dots\ ,\ b_{7})$ et la formule (*)
- Tester la fonction pour retrouver, au passage, le résultat de la question 2
# Réponse
Attaque sur un LFSR : reconstruction du polynôme de rétroaction minimal¶
Si l'attaquant dispose des 16 premiers bits $b_0,\ \dots\ ,\ b_{15}$, il peut reconstruire le polynôme de rétroaction $f(X) = 1 + c_1X + \dots + c_8X^8$.
Il suffit, en effet, de résoudre l'équation matricielle : $$ \left(\begin{array}{cccc} b_0 & b_1 & \dots & b_7 \\ b_1 & b_2 & \dots & b_8 \\ \vdots & & & \vdots \\ b_7 & b_8 & \dots & b_{14} \\ \end{array}\right) . \left(\begin{array}{c} c_8 \\ c_7 \\ \vdots \\ c_1 \\ \end{array}\right) = \left(\begin{array}{c} b_8 \\ b_9 \\ \vdots \\ b_{15} \\ \end{array}\right) $$
Pour cela, on peut utiliser la méthode du pivot de Gauss pour résoudre le système d'équations linéaires associé d'inconnues $c_8,\ \dots\ ,\ c_1$.
On résume ce système avec la "matrice étendue" $\left(\begin{array}{cccc | c} b_0 & b_1 & \dots & b_7 & b_8 \\ b_1 & b_2 & \dots & b_8 & b_9 \\ \vdots & & & & \vdots \\ b_7 & b_8 & \dots & b_{14} & b_{15} \\ \end{array}\right)$.
On applique alors l'algorithme suivant :
Pour $i$ variant de 0 à 7 :
si la ligne $i$ ne contient pas 1 en position $i$, on cherche une ligne $k$ contenant 1 en position $i$ et on remplace la ligne $i$ par son XOR avec la ligne $k$
on remplace chaque ligne qui contient 1 en colonne $i$, sauf la $i$-ième, par son XOR avec la ligne $i$ $$ $$
Si la boucle s'est bien terminée, on obtient l'unique solution dans la dernière colonne (attention à l'ordre)
Si le premier point dans la boucle échoue, c'est que la matrice n'est pas inversible car la complexité linéaire est en fait strictement inférieure à 8...
Dans ce cas, pour déterminer la complexité linéaire et le polynôme de rétroaction minimal, on exécute l'algorithme précédent pour toutes les complexités linéaires $l$ possibles $1,\ \dots,\ 7$ en partant de $l=1$, jusqu'à pouvoir reconstituer tous les termes connus de la suite.
Chaque résolution de système, à partir des $2l$ premiers bits $b_0,\ \dots,\ b_{2l-1}$ fournit un polynôme de rétroaction candidat que l'on teste avec les termes suivants de la suite $b_{2l},\ \dots,\ b_{15}$ pour savoir s'il convient.
Question 5 :
- Programmer une fonction attaque_LFSR$(lst)$ qui retourne la complexité linéaire (inférieure ou égale à 8) et le polynôme de rétroaction minimal à partir de la liste $lst$ des $2l$ premiers bits $b_0,\ \dots,\ b_{2l-1}$
- Tester la fonction avec notre LFSR
# Réponse