Générateurs de nombres aléatoires
TP3 - Générateur à signal d'arrêt et générateur de Geffe
TP3 - Générateur à signal d'arrêt et générateur de Geffe
Exercice 1 : le générateur à signal d'arrêt¶
Le générateur à signal d'arrêt est un exemple de registre à décalage irrégulier (1984). Il utilise la sortie d'un premier LFSR $R_1$ pour contrôler l'horloge d'un second LFSR $R_2$. Plus précisément, $R_2$ ne change d'état à l'instant $t$ que si la sortie de $R_1$ est égale à 1 à l'instant $t-1$, autrement dit si la sortie de $R_1$ est égale à 0 à l'instant $t-1$, alors $R_2$ n'est pas décalé et le bit de sortie à l'instant $t$ est donc toujours égal au bit de sortie à l'instant $t-1$.

Question 0 (à la main) :
En supposant que $R_1$ et $R_2$ produisent des séquences uniformément distribuées, calculer la probabilité que deux bits consécutifs produits par le générateur à signal d'arrêt soient égaux.
Réponse :
Question 1 :
Définir une fonction permettant de simuler un tel générateur, puis estimer cette probabilité.
# Réponse
Question 2 :
Un adversaire a intercepté le chiffré suivant :
$c = 0000\ 1111\ 1101\ 1010\ 0111\ 1101\ 0101\ 1001$
Il sait qu'il s'agit du chiffrement de l'un des trois textes suivants à l'aide d'un générateur à signal d'arrêt :
$m_1 = 0110\ 1001\ 0010\ 1001\ 0101\ 1001\ 0110\ 0001$
$m_2 = 0110\ 0010\ 1111\ 0100\ 1010\ 1011\ 1111\ 0101$
$m_3 = 1110\ 1000\ 0101\ 1101\ 1001\ 1110\ 1100\ 0101$
Donner le texte clair qui a été le plus probablement chiffré.
# Réponse
Exercice 2 : le générateur de Geffe¶
Le générateur de Geffe est un exemple de registres combinés (1973). Il est compoé de trois LFSR de longueurs distinctes combinés par la fonction :
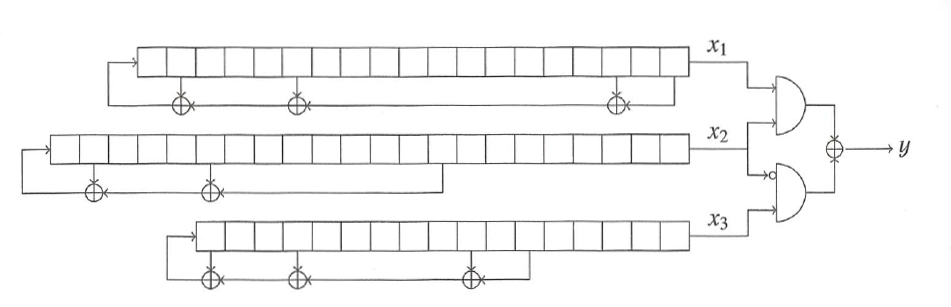
En 1985, T. Siegenthaler a proposé une méthode de cryptanalyse sur les systèmes de chiffrement par flot par registres combinés appelé attaque par corrélation. L'idée de cette méthode est d'exploiter l'existence d'une éventuelle corrélation entre la suite chiffrante et le contenu de certains registres. Un attaquant peut alors chercher séparément les valeurs initiales de chaque registre et retrouver la clé plus rapidement qu'en effectuant une recherche exhaustive. Le but de l'exercice est de montrer que le générateur de Geffe est vulnérable à une telle attaque.
Question 1 (à la main) :
En supposant que les valeurs $x_i(t)$ suivent des lois de Bernoulli indépendantes de paramètre $\frac{1}{2}$, montrer que :
$P\big(y(t) = x_1(t)\big) = \frac{3}{4} = P\big(y(t) = x_3(t)\big)$
Réponse :
Question 2 :
Définir une fonction permettant de simuler un tel générateur, puis estimer ces deux probabilités.
# Réponse
Question 3 :
En supposant connue la sortie du générateur (et les 3 polynômes de rétroaction), proposer une attaque par corrélation pour déterminer la clé c'est à dire la graine ou encore les états initiaux de $R_1$, $R_2$ et $R_3$.
Une attaque par force brute serait en $O\big(2^{l_1+l_2+l_3}\big)$ où $l_i$ désigne la longueur de $R_i$.
L'attaque par corrélation demandée est en $O\big(2^{l_1}+2^{l_3}+2^{l_2}\big)$ voire en $O\big(2^{l_1}+2^{l_3}+l_2^3\big)$.D'autres attaques sont connues :
- l'attaque "deviner et déterminer" en $O\big(2^{l_2}\left(l_1^3+l_3^3\right)\big)$
- l'attaque algébrique en $O\big(\left(l_1+l_2+l_3\right)^6\big)$
# Réponse