Générateurs de nombres aléatoires
TP4 - Générateur A5/1 (GSM)
TP4 - Générateur A5/1 (GSM)
Le système A5/1 est un exemple de registres combinés où le décalage des registres est irrégulier. Il est composé de trois LFSR (de longueurs 19, 22 et 23 bits) combinés par $\oplus$. L'horloge de chacun de ces registres est contrôlée par une fonction de transition particulière : le système calcule la fonction "majorité" de trois bits (appelés bits d'horloge) à des positions fixes, et seuls les registres ayant le bit d'horloge qui a emporté la majorité sont décalés.
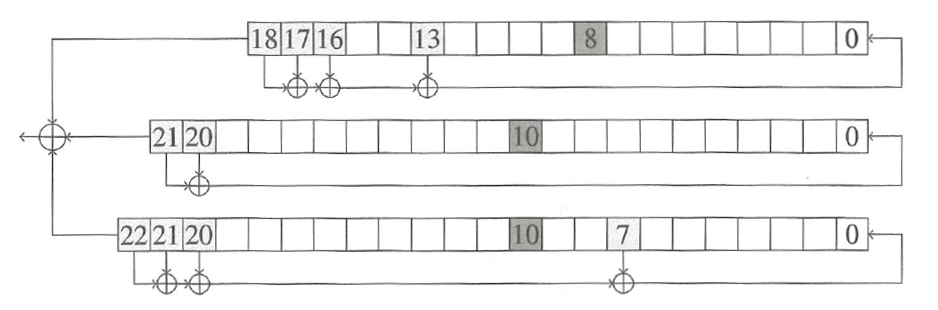
Etats internes de A5/1¶
Soit $E\in \mathbb F_2^{64}$ un état interne pour A5/1 (les 19 premiers bits correspondent au contenu de $R_1$, les 22 suivants à celui de $R_2$ et les 23 derniers à celui de $R_3$).
On considère la v.a. $n_E$ égale au nombre d'états internes donnant $E$ après une transition de A5/1.
On souhaite, dans cette partie, calculer l'espérance de $n_E$.
Pour déterminer le décalage des registres lors d'une transition de A5/1, nous avons deux configurations possibles :
- soit les trois bits d'horloge ont la même valeur $b$
- soit seulement deux sont égaux à $b$ et le troisième à $1-b=\bar b$
Le diagramme suivant illustre l'évolution de l'état interne en fonction de ces deux configurations :
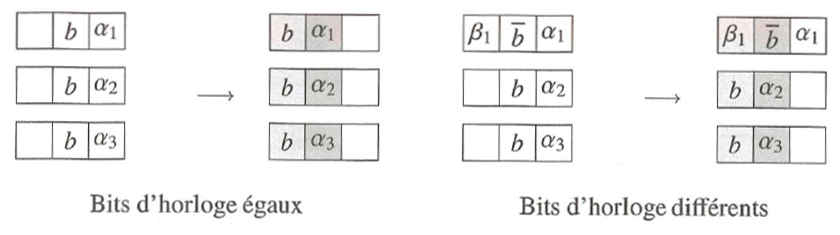
Le nombre d'états produisant un état $E$ dépend donc uniquement :
- des bits d'horloge $h_1, h_2, h_3$ aux positions $8, 10, 10$ dans $R_1, R_2, R_3$ repectivement (en gris foncé)
- des bits $g_1, g_2, g_3$ situés à gauche c'est à dire aux positions $9, 11, 11$ dans $R_1, R_2, R_3$ repectivement (en gris clair)
En raisonnant ainsi pour les 64 choix possibles des vecteurs $(h_1, h_2, h_3)$ et $(g_1, g_2, g_3)$, nous obtenons $n_E$.
Pour toutes les configurations où $g_1=0$ (on a la même distribution quand $g_1=1$), le tableau suivant présente les résultats :
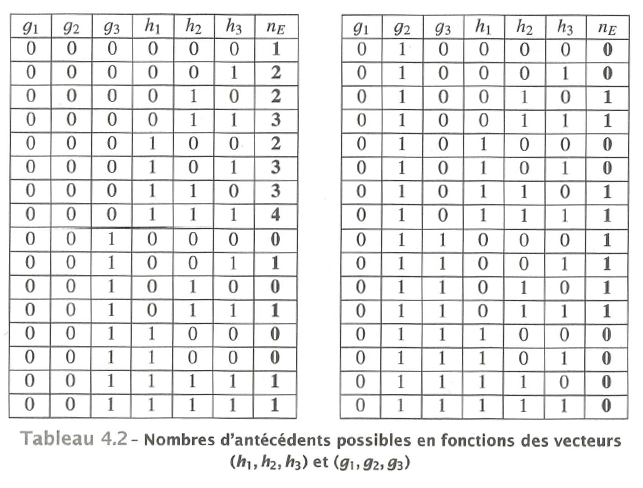
Question 1 (à la main) :
Justifier le calcul de $n_E$ dans les configurations suivantes :
- $(g_1, g_2, g_3) = (0,0,1)$ et $(h_1, h_2, h_3) = (0,0,0)$
- $(g_1, g_2, g_3) = (0,0,0)$ et $(h_1, h_2, h_3) = (0,0,0)$
- $(g_1, g_2, g_3) = (0,0,0)$ et $(h_1, h_2, h_3) = (0,0,1)$
- $(g_1, g_2, g_3) = (0,0,0)$ et $(h_1, h_2, h_3) = (0,1,1)$
- $(g_1, g_2, g_3) = (0,0,0)$ et $(h_1, h_2, h_3) = (1,1,1)$
Réponse :
Question 2 (à la main) :
En déduire la loi de $n_E$ et calculer son espérance.
Réponse :
Attaque par compromis temps-mémoire sur A5/1¶
En utilisant la propriété précédente, J.D. Golic a montré (1997) que le système de chiffrement par flot $A5/1$ est vulnérable aux attaques par compromis temps-mémoire. Ce type d'attaque se trouve à mi-chemin entre une recherche exhaustive de l'état interne des registres et un stockage complet préalable de tous les états internes possibles correspondant à une chaîne de la suite chiffrante. Plus précisément, elle s'appuie sur l'algorithme suivant :

La complexité de l'attaque est de :
- $T.128$ bits en mémoire
- $T$ évaluations de $A5/1$ pour calculer les vecteurs $\vec a_i$ dans la première étape de l'algorithme (construction de la liste $L$)
- $l$ recherches dans la liste $L$ dans la seconde étape de l'algorithme
Le coût en temps de ces deux étapes est équilibré pour $l=T=2^{32}$. De plus, on peut montrer que si $l.T=2^{64}$, l'algorithme réussit avec une probabilité proche de 1. L'attaquant dispose alors d'un état interne $E$ et d'une valeur $t$ tels que $E$ produit la suite chiffrante attaquée à partir de l'indice $t$. En inversant la fonction de transition comme dans la première partie de l'exercice, l'adversaire obtient l'état interne initial (et donc la clé).
Question 3 :
Implémenter cet algorithme.
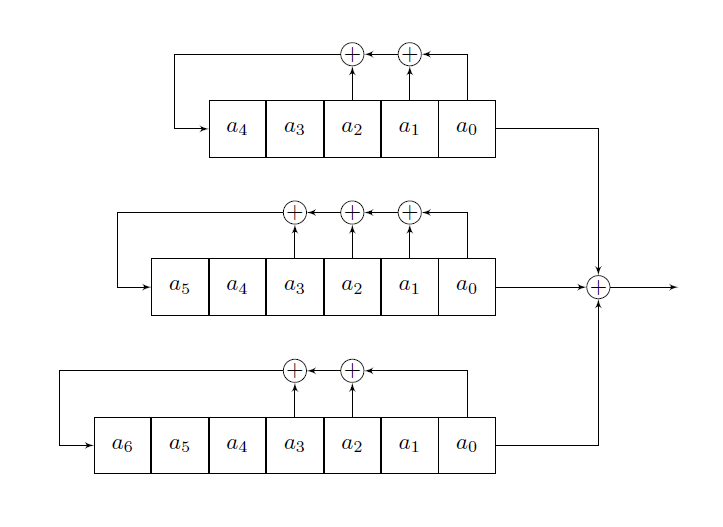
Pour le tester, on pourra considérer le générateur ci-dessous fonctionnant sur le même principe que le A5/1 en prenant pour les bits d'horloge dans $R_1$, $R_2$ et $R_3$ respectivement $a_3$, $a_4$ et $a_4$. On remplacera alors 64 par 18 et on prendra $l=T=2^{9}$.
# Réponse