Introduction aux courbes elliptiques
TP - Représentation de courbes et de surfaces

2019/2020 - A. RIDARD

import numpy as np
import pylab as pl
from mpl_toolkits.mplot3d import Axes3D

Coniques

Représenter les trois coniques (pour certaines valeurs des paramètres $p,a,b$) :

• parabole : $y^2=2px$
• ellipse : $\displaystyle\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$
• hyperbole : $\displaystyle\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$

# Réponse

Quadriques

Représenter les quadriques des exercies 9 et 10 :

• paraboloïde elliptique : $z=x^2+y^2$
• paraboloïde hyperbolique : $z=x^2-y^2$
• ellipsoïde : $x^2+y^2+z^2=1$
• hyperboloïde à une nappe : $x^2+y^2-z^2=1$
• hyperboloïde à deux nappes : $x^2-y^2-z^2=1$
• cône du second degré : $x^2+y^2-z^2=0$

# Réponse

Courbes elliptiques

Représenter les courbes d'équation $y^2=x^3+ax+b$ sur $[-3,3]^2$ (pour certaines valeurs des paramètres $a,b$) comme sur l'article de Wikipédia.

# Réponse

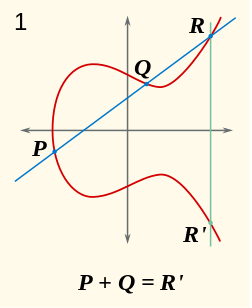
Loi de groupe

Représenter la loi de groupe dans le cas général ($P\neq Q$ et $x_1\neq x_2$) comme ci-dessous, et dans le cas où $P=Q$, en vous aidant du dernier TD.

# Réponse