Probabilités
TP 2 - Variables aléatoires finies
TP 2 - Variables aléatoires finies
# importation des modules
import numpy as np
import numpy.random as npr
import scipy.stats as sps
import matplotlib.pyplot as plt
Remarque :
- Pour calculer les lois de probabilité (pmf ou pdf) et les fonctions de répartition (cdf), on utilisera scipy.stats (sps)
- Pour générer des tableaux de nombres aléatoires, on utilisera numpy.random (npr)
Lois usuelles finies : le point de vue théorique¶
Dans cette partie, nous allons représenter graphiquement les trois lois usuelles finies vues en cours.
Loi uniforme (sps.randint) sur $\{1,...,6\}$¶
fig, (ax1, ax2) = plt.subplots(1, 2)
plt.tight_layout(rect = [0, 0, 1, 0.85])
plt.suptitle('Loi uniforme sur $\{1,...,6\}$', fontsize=16)
ax1.set_title('Loi de probabilité')
ax1.set_ylim(-0.05, 1)
a = 1
b = 6
x = np.arange(a,b+1)
y = sps.randint.pmf(x, a, b+1)
ax1.stem(x, y)
ax2.set_title('Fonction de répartition')
x = np.linspace(-1, b+1, int(1e3))
y = sps.randint.cdf(x, a, b+1)
ax2.plot(x, y)
plt.show()
Loi de Bernoulli (sps.bernoulli) de paramètre $p = 0.3$¶
# Réponse
Loi binomiale (sps.binom) de paramètres $n = 20$ et $p = 0.3$¶
# Réponse
Lois usuelles finies : le point de vue empirique¶
Dans cette partie, nous allons effectuer nos premières simulations pour approcher les espérances vues en cours.
Utilisation des générateurs fournis par numpy.random (npr)¶
Pour chacune des lois suivantes :
- Simuler 100 réalisations à l'aide du générateur adapté
- Calculer la moyenne de ces 100 valeurs
- Comparer cette moyenne empirique avec la moyenne théorique (espérance) vue en cours
Loi uniforme (npr.randint) sur $\{1,...,6\}$
# Réponse
Loi de Bernoulli (npr.binomial) de paramètre $p = 0.3$
# Réponse
Loi binomiale (npr.binomial) de paramètres $n = 20$ et $p = 0.3$
# Réponse
Définition de nos propres générateurs à partir de celui de la loi uniforme sur [0,1[ (npr.rand)¶
Loi uniforme sur $\{1,...,6\}$
- A l'aide de npr.rand, définir une fonction myRandint qui génère un tableau de nombres aléatoires (selon la loi considérée)
- Simuler 100 réalisations à l'aide de ce générateur
- Comparer la moyenne empirique avec la moyenne théorique
# Réponse
Loi de Bernoulli de paramètre $p = 0.3$
- A l'aide de npr.rand, définir une fonction myBernoulli qui génère un tableau de nombres aléatoires (selon la loi considérée)
- Simuler 100 réalisations à l'aide de ce générateur
- Comparer la moyenne empirique avec la moyenne théorique
# Réponse
Loi binomiale de paramètres $n = 20$ et $p = 0.3$
- A l'aide de myBernoulli, définir une fonction myBinomial qui génère un tableau de nombres aléatoires (selon la loi considérée)
- Simuler 100 réalisations à l'aide de ce générateur
- Comparer la moyenne empirique avec la moyenne théorique
# Réponse
Remarque : on peut en fait simuler toutes les lois usuelles, même les lois continues, à l'aide de la seule loi uniforme sur [0,1[ !
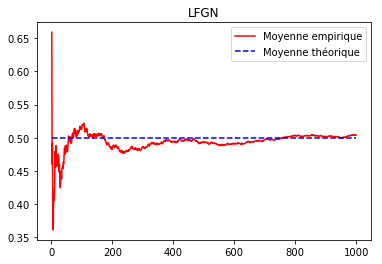
Loi Forte des Grands Nombres¶
Nous avons observé, pour trois lois usuelles finies, que la moyenne empirique (pour 100 réalisations) était proche de la moyenne théorique.
En fait, ce résultat se généralise au travers du théorème de la Loi Forte des Grands Nombres (LFGN).
Théorème (LFGN) :
Soit $X_i$ des v.a. indépendantes et de même loi (éventuellement inconnue) d'espérance $m$.
Alors, la moyenne empirique converge (presque sûrement) vers la moyenne théorique :
$$\bar X_n=\displaystyle\frac{1}{n}\sum_{i=1}^{n}X_i\xrightarrow[n\to+\infty]{(p.s.)}m$$
En pratique, on considère que la moyenne empirique (pour $n$ assez grand) est proche de la moyenne théorique
Ecrire un script permettant d'illustrer ce théorème de la manière suivante, par exemple avec les $X_i$ de loi uniforme sur [0,1[.
# Réponse
Remarque : si les $X_i\sim \mathcal B(p)$, alors la LFGN légitime l'approximation d'une probabilité par une fréquence empirique !
Justifier cette remarque
Réponse :
Théorème Central Limite¶
Nous savons maintenant (LFGN) que la moyenne empirique (pour $n$ assez grand) est "proche" de la moyenne théorique, mais comment se distribue-t-elle ?
Autrement dit, si l'on calcule plusieurs moyennes empiriques (pour un même $n$ assez grand), comment se répartissent-elles autour de la moyenne théorique ?
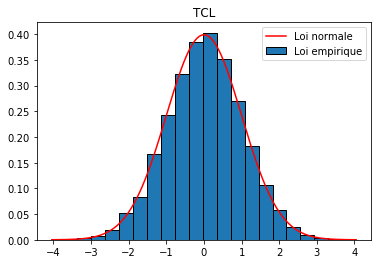
C'est le Théorème Central Limite (TCL) qui répond à cette question.
Théorème (TCL) :
Soit $X_i$ des v.a. indépendantes et de même loi (éventuellement inconnue) d'espérance $m$ et d'écart-type $\sigma$.
Alors, la moyenne empirique centrée réduite converge (en loi) vers la gaussienne centrée réduite :
$$\displaystyle\frac{\bar X_n-m}{\frac{\sigma}{\sqrt{n}}}\xrightarrow[n\to +\infty]{\mathcal L}\mathcal N(0,1)$$
En pratique, on considère que la loi de la moyenne empirique centrée-réduite est proche de la loi normale centrée-réduite.
Ecrire un script permettant d'illustrer ce théorème de la manière suivante, par exemple avec les $X_i$ de loi uniforme sur [0,1[.
# Réponse
Remarque : le TCL est à la base de la statistique inférentielle...
Application de la Loi Forte des Grands Nombres : résolution par simulation¶
Un test permet de détecter la grippe aviaire sur les poulets. Cependant, ce test n’est pas parfait car si un poulet n’est pas infecté, le test est positif avec probabilité 0,02 et lorsque le poulet est infecté, le test est négatif avec probabilité 0,01. On sait également que 10% des poulets sont infectés.
On note $I$ l'événement " le poulet est infecté " et $T$ l'événement " le test est positif ".
Sachant que le test est positif sur un poulet, quelle est la probabilité que ce poulet soit infecté ?
# Votre réponse
On choisit au hasard, successivement et avec remise, 10 poulets non infectés.
On note $X$ le nombre de poulets testés positifs.
Déterminer la loi de $X$.
# Votre réponse
Calculer la probabilité d’obtenir 2 poulets testés positifs.
# Votre réponse
Combien de poulets testés négatifs peut-on espérer obtenir ?
# Votre réponse