TP4 - turtle : introduction à la boucle for

A. Ridard

Activité

Commencez par importer les fonctions de la bibliothèque turtle, puis ouvrez une fenêtre graphique.

# Réponse

Dessinez un triangle de côté 100 en remettant la tortue dans sa position initiale (à l'origine et orientée par l'axe des abscisses).

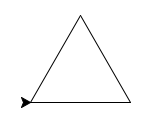
# Réponse

# on efface

resetscreen()

Combien de fois répétez-vous la même séquence d'instructions ?

Présentation

En programmation, il est possible de répéter plusieurs fois une instruction, et même un bloc d'instructions (même niveau d'indentation) grâce à la boucle for.

Dans le code suivant, le bloc d'instructions est exécuté 5 fois.

forward(100)

for i in range(5): 
    write(i)
    forward(20)
    left(90)
    forward(20)
    right(90)

forward(100)

# on efface

resetscreen()

Dans l’expression for i in range(5), le i est appelé variable d’itération ou compteur de boucle.
Par défaut, ce compteur commence à 0 et augmente de 1 à chaque "tour de boucle" jusqu’à 5-1 = 4.

/!\ La valeur maximale prise par le compteur de boucle est le paramètre de range() diminué de 1.

L'instruction write(i) permet d'écrire la valeur de i sur le dessin, de manière à visualiser son évolution.

Exercices (automatiser un dessin)

Cette boucle for va nous permettre de simplifier le dessin des formes symétriques.

Exercice 1 (polygones réguliers)

Dessiner un triangle de côté 100

# réponse

# on efface

resetscreen()

Dessiner un carré de côté 100

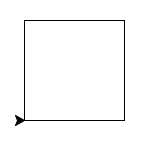
# réponse

# on efface

resetscreen()

Dessiner un pentagone de côté 100

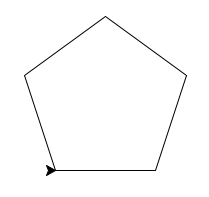
# réponse

# on efface

resetscreen()

Dessiner un hexagone de côté 100

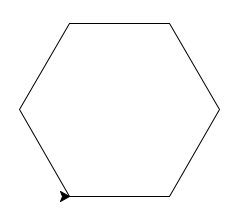
# réponse

# on efface

resetscreen()

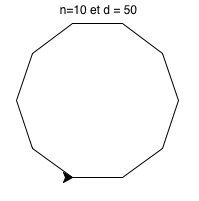
Ecrire un programme :

• qui demande à l'utilisateur de saisir un entier n inférieur à 20, puis un entier d inférieur à 100
• qui dessine le polygone régulier à n côtés de longueur d

# réponse

# on efface

resetscreen()

Exercice 2 (losange et fleur)

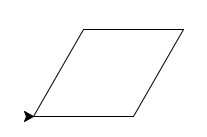
Dessiner un losange de côté 100 dont les angles valent 60° et 120°.

# réponse   

# on efface

resetscreen()

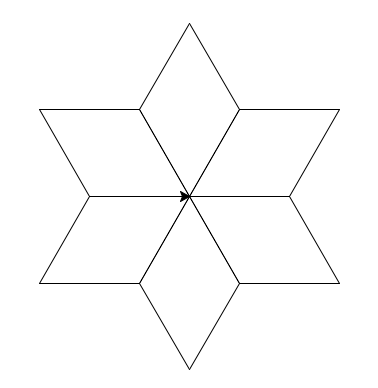
Dessiner 6 fois ce losange pour représenter une fleur.

# réponse

# on efface

resetscreen()

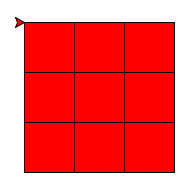
Exercice 3 (face du cube de Rubik)

Dessiner une face du cube, par exemple la face rouge.

# réponse

# on efface

resetscreen()