TP7 - Booléens et branchement conditionnel if

A. Ridard

Booléens

Les booléens de type bool ont deux valeurs possibles : True et False.

On les rencontre par exemple lorsque l'on fait des comparaisons.

Egalité

1 == 1

Différence

1 != 2

Inégalité stricte

1 > 2

Inégalité large

1 <= 1

On peut appliquer les opérateurs logiques aux booléens :

• la négation not
• la conjonction and
• la disjonction or
• le OU EXCLUSIF ^

Voici les tables de vérité qui résument les comportements de ces opérateurs :

$$\begin{array}{|c||c|} \hline P & \textrm{\textbf{not}} (P) \\ \hline \hline V & F \\ \hline F & V \\ \hline \end{array} \hspace{1cm} \begin{array}{|c|c||c|} \hline P & Q & P \textrm{ \textbf{and} } Q \\ \hline \hline V & V & V \\ \hline V & F & F \\ \hline F & V & F \\ \hline F & F & F \\ \hline \end{array} \hspace{1cm} \begin{array}{|c|c||c|} \hline P & Q & P \textrm{ \textbf{or} } Q \\ \hline \hline V & V & V \\ \hline V & F & V \\ \hline F & V & V \\ \hline F & F & F \\ \hline \end{array} \hspace{1cm} \begin{array}{|c|c||c|} \hline P & Q & P \textrm{ \textbf{xor} } Q \\ \hline \hline V & V & F \\ \hline V & F & V \\ \hline F & V & V \\ \hline F & F & F \\ \hline \end{array}$$

not(True) 

True and False

True or False

True ^ False

(1 <= 2) == (1<2 or 1==2)

Branchement conditionnel if

Le branchement conditonnel if permet de soumettre l'exécution d'un bloc d'instructions à une condition.

Cette dernière est exprimée à l'aide de comparaisons (==, !=, <, <=, >, >=) pouvant être combinées avec les opérateurs logiques.

Exemple 1 : si ..., alors ...

n = input("Saisir un entier :")
n = int(n)

if n > 0 :
    print("Positif")

Exemple 2 : si ..., alors ..., sinon ...

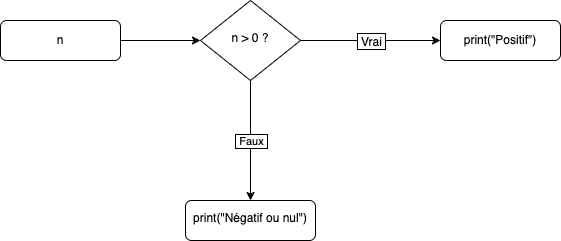
n = input("Saisir un entier :")
n = int(n)

if n > 0 :
    print("Positif")
else :
    print("Négatif ou nul")

print("Le programme continue quelque soit la branche sélectionnée")

Exemple 3 : branchements imbriqués

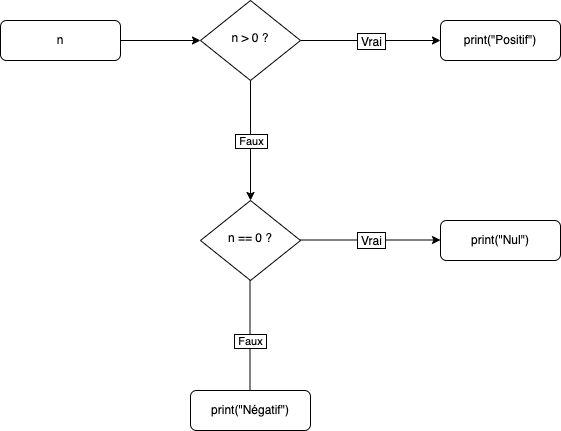
n = input("Saisir un entier :")
n = int(n)

if n > 0 :
    print("Positif")
else :
    if n == 0 :
        print("Nul")
    else :
        print("Négatif")

print("Le programme continue quelque soit la branche sélectionnée")

Exemple 4 : condition combinée avec and

n = input("Saisir un entier :")
n = int(n)

if n > 0 and n%2 == 0 :
    print("Positif et pair")

print("Le programme continue même si aucune branche n'a été sélectionnée")

Exercices

Exercice 1 : le Mölkky

Ecrire un programme :

• qui demande à l'utilisateur de saisir son ancien score ainsi que son gain
• qui affiche le résultat selon les règles suivantes :

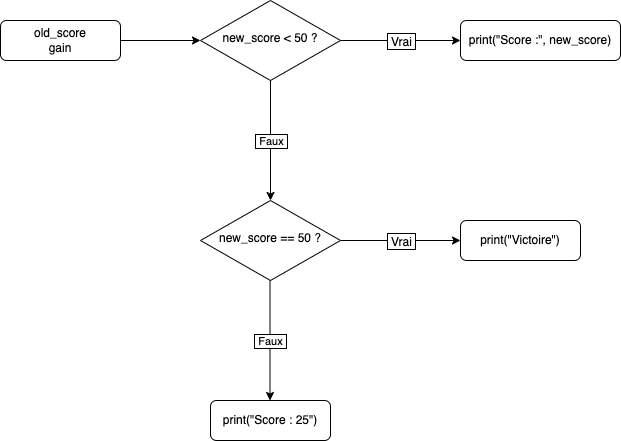
# Réponse

Exercice 2 : promotion en 2M (version 1)

Ecrire un programme :

• qui demande à l'utilisateur de saisir son total de points, son "panier" et son nombre de notes insuffisantes
• qui affiche soit réussite, soit échec

# Réponse

Exercice 3 : recherche du plus petit élément d'une liste

Ecrire un programme qui affiche le plus petit élément d'une liste d'entiers.

Pour tester votre programme, voici une liste de 50 entiers inférieurs à 500, générée au hasard grâce à la bibliothèque numpy.random

import numpy.random as npr

lst_entiers = npr.randint(0, 500, 50)
print(lst_entiers)

# Réponse

Exercice 4 : promotion en 2M (version 2)

Ecrire un programme :

• qui demande à l'utilisateur de saisir ses 11 moyennes (Français, L2, L3, Maths, Info, Chimie, Physique, Histoire, Eco droit, Art visuel ou Musique, OS)
• qui affiche soit réussite, soit cas limite, soit échec

# Réponse