TP2 - Cryptographie

A. Ridard

Chiffrement par décalage, dit "chiffrement de César"

# Voici une variable globale et deux fonctions utiles pour cette section

alphabet = "abcdefghijklmnopqrstuvwxyz"

def lettreToEntier(lettre) :
    return alphabet.find(lettre)

def entierToLettre(i) :
    return alphabet[i]

print("Lettre -> entier : w ->", lettreToEntier('w'))
print("Entier -> Lettre : 22 ->", entierToLettre(22))

Fonction de chiffrement

Définir une fonction chiffrementDecalage(m, k) qui retourne le (message) chiffré de m moyennant la clé k.

# réponse

# test

try :
    assert chiffrementDecalage("messageenclair",3) == "phvvdjhhqfodlu"
    assert chiffrementDecalage("venividivici",-3) == "sbkfsfafsfzf"
    print("chiffrementDecalage : OK")
except :
    print("chiffrementDecalage : ERREUR")

Fonction de déchiffrement

Définir une fonction dechiffrementDecalage(c, k) qui retourne le (message) clair de c moyennant la clé k.

# réponse

# test

try :
    assert dechiffrementDecalage("phvvdjhhqfodlu",3) == "messageenclair"
    assert dechiffrementDecalage("sbkfsfafsfzf",-3) == "venividivici"
    print("dechiffrementDecalage : OK")
except :
    print("dechiffrementDecalage : ERREUR")

Deux Attaques

Attaque par force brute

Ce type d'attaque, appelée aussi attaque exhaustive, consiste à essayer toutes les clés possibles. Un mécanisme de chiffrement utilisant un trop petit nombre de clés est donc facilement cassable avec cette technique.

A ce propos, voici un élément de réflexion sur la robustesse des mots de passe :

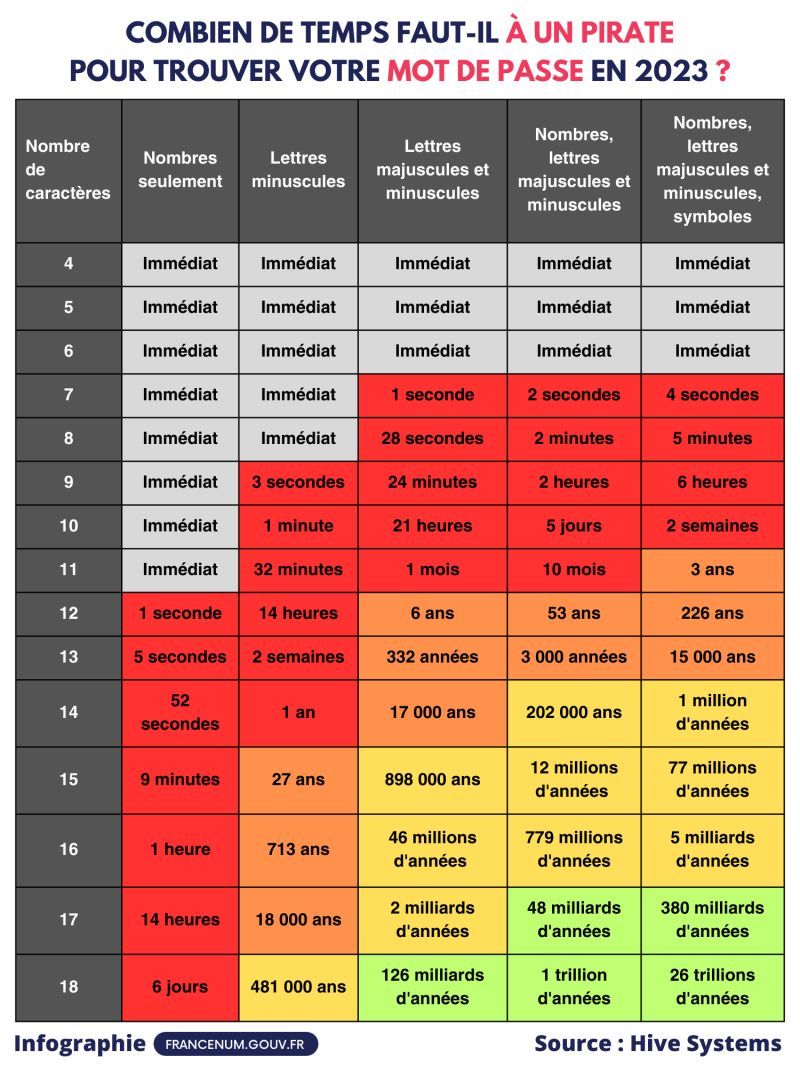
Définir une fonction attaqueForceBrute(c) qui décrypte le chiffré c.

# réponse

# test

attaqueForceBrute("phvvdjhhqfodlu")

Attaque par analyse fréquentielle

Lorsque l'attaque par force brute se montre moins efficace (pensez à un chiffrement par substitution polyalphabétique comme celui de Vigenère), l'attaque par analyse fréquentielle permet de décrypter le chiffré assez rapidement.

Dans sa forme la plus simple (attaque du chiffrement de César), elle consiste à déterminer la lettre la plus fréquente dans le chiffré, et d'en déduire la clé en calculant le décalage avec la lettre "e" qui est la plus fréquente dans la langue française, et donc probablement aussi la plus fréquente dans le clair.

Cette dernière affirmation est "presque toujours" vraie lorsque le message est assez long, d'après la loi forte des grands nombres (résultat statistique fondamental au même titre que le théroème central limite).

Comme souvent en Informatique, nous allons découper le problème en sous-problèmes ayant chacun une fonction comme réponse.

Définir une fonction frequenceLettre(lettre, txt) qui retourne la fréquence (en %) du caractère lettre dans le texte txt.

# réponse

# test

chiffre = "abhffbzzrfpbzzrqrfanvafnffvffheqrfrcnhyrfqrtrnagffvabhfiblbafcyhfqrpubfrfrgcyhfrybvtarrfdhrhkprarfgcnfnpnhfrqryncrefcvpnpvgrqrabgerihravqrabgertenaqrheprfgcneprdhrabhffbzzrfryrirfcnerhk"

try :
    assert round(frequenceLettre('f',chiffre),2) == 15.68
    assert round(frequenceLettre('a',chiffre),2) == 7.03
    print("frequenceLettre : OK")
except :
    print("frequenceLettre : ERREUR")

Définir une fonction frequenceTouteLettre(txt) qui retourne la fréquence (en %) de chaque lettre de l'alphabet dans le texte txt, sous la forme d'un dictionnaire ayant pour clé chaque lettre, et pour valeur la fréquence correspondante.

# réponse

# test

print("Fréquence de chaque lettre dans le chiffré :", frequenceTouteLettre(chiffre))

Définir une fonction triFreq(dict_freq) qui retourne le dictionnaire des fréquences trié dans l'ordre décroissant, sous forme d'une liste de couples : [ ('e', 17.39), ('a', 8.15), ... ]

# réponse

# test

# Commençons par stocker dans une variable globale le dictionnaire des fréquences en français
# Source : https://www.apprendre-en-ligne.net/crypto/stat/francais.html

dict_freq_francais = {'a': 8.15, 'b': 0.97, 'c': 3.15, 'd': 3.73, 'e': 17.39, 
                     'f': 1.12, 'g': 0.97, 'h': 0.85, 'i': 7.31, 'j': 0.45, 
                     'k': 0.02, 'l': 5.69, 'm': 2.87, 'n': 7.12, 'o': 5.28, 
                     'p': 2.80, 'q': 1.21, 'r': 6.64, 's': 8.14, 't': 7.22, 
                     'u': 6.38, 'v': 1.64, 'w': 0.03, 'x': 0.41, 'y': 0.28, 
                     'z': 0.15}

triFreq(dict_freq_francais)

Définir une fonction getNiemelettre(dict_freq, n) qui retourne la n-ième lettre la plus fréquente d'après dict_freq.

# réponse

# test

try :
    assert getNiemeLettre(frequenceTouteLettre(chiffre),1) == 'r'
    assert getNiemeLettre(dict_freq_francais,1) == 'e'
    assert getNiemeLettre(dict_freq_francais,2) == 'a'
    assert getNiemeLettre(dict_freq_francais,3) == 's'
    print("getNiemeLettre : OK")
except :
    print("getNiemeLettre : ERREUR")

Définir une fonction calculeDecalage(lettre1, lettre2) qui retourne le décalage (modulo 26) permettant de passer de lettre1 à lettre2.

# réponse

# test

try :
    assert calculDecalage('a','d') == 3
    assert calculDecalage('d','a') == 23
    assert calculDecalage('z','c') == 3
    assert calculDecalage('r','a') == 9
    print("calculDecalage : OK")
except :
    print("calculDecalage : ERREUR")

Définir une fonction attaqueAnalyseFreq(c) qui décrypte le chiffré c.

# réponse

# test 1

attaqueFrequenceDec(chiffre)

# test 2

chiffre2 = "vcfgrwqwoizcuwgtowbsobhgoizcuwgsghqseisqsghoixcifrviwxcifrstshsqcaasbhsghqseisjcigbsgojsndogeishobhrsgofhwgobgjcigbsrsjsndogjcigacbhfsfibxcifcijfwsfgobgojcwfzsgwbgwubsgrsjcgdfctsggwcbgdofzshcweiszsghhcbashwsf"
attaqueFrequenceDec(chiffre2)

Remarque : si le message n'est pas assez long, la lettre la plus fréquente dans le chiffré peut ne pas correspondre à la lettre "e". Dans ce cas, on peut essayer de calculer le décalage entre la deuxième lettre la plus fréquente dans le chiffré et la lettre "e"...

Chiffrement par LFSR

# Voici deux fonctions utiles pour cette section

def stringToBinary(msg) :
    msg_bin = ""
    for i in bytearray(msg, encoding ='ascii') :
        msg_bin = msg_bin + format(i, '08b')
    return msg_bin

def binaryToString(binary) :
    msg = ""
    for i in range(0, len(binary), 8) :
        byte_int = int(binary[i:i+8], 2)
        byte_char = chr(byte_int)
        msg = msg + byte_char   
    return msg

        
print("En binaire :", stringToBinary("message en clair"))
print("En ascii :", binaryToString(stringToBinary("message en clair")))

Masque jetable de Vernam

Définir une fonction chiffrementVernam(m, k) qui retourne le chiffré de m moyennant la clé k.

# réponse

# test

try :
    assert chiffrementVernam(stringToBinary("vernam"),"110011001100110011001100110011001100110011001100") == "101110101010100110111110101000101010110110100001"
    print("chiffrementVernam : OK")
except :
    print("chiffrementVernam : ERREUR")

Déchiffrer le message "1010001010101101101010011011111010111000" ayant été chiffré avec la clé "1100110011001100110011001100110011001100".

LFSR

Définir une fonction etatSuivant(etat, coeff) qui retourne l'état suivant du registre et le bit de sortie sous la forme d'un couple.

Elle prend en paramètres l'état actuel du registre sous la forme d'une liste (binaire), et les positions des coefficients de rétroaction non nuls sous la forme d'une liste d'entiers (cf. test pour des exemples).

# réponse

# test
    
try :
    assert etatSuivant([1,0,0,1],[0,2,3]) == ([0, 1, 0, 0],1)
    assert etatSuivant(etatSuivant([1,0,0,1],[0,2,3])[0],[0,2,3]) == ([0, 0, 1, 0],0)
    print("etatSuivant : OK")
except :
    print("etatSuivant : ERREUR")

Définir une fonction suiteChiffrante(k, coeff, n) qui retourne la suite chiffrante sous la forme d'une chaine de caractères.

Elle prend en paramètres l'état initial du registre (clé k), les positions des coefficients de rétroaction non nuls, et la longueur souhaitée de la suite chiffrante.

# réponse

# test

try :
    assert suiteChiffrante([1,0,0,1],[0,2,3],14) == "10010010010010"
    print("suiteChiffrante : OK")
except :
    print("suiteChiffrante : ERREUR")

Définir une fonction chiffrementLFSR(m, k, coeff) qui retourne le chiffré de m moyennant la clé k et les positions des coefficients de rétroaction non nuls.

# réponse

# test

try :
    assert chiffrementLFSR("50ansGyYv",[1,0,0,1],[0,2,3]) == "101001110111100101000101111111000011101001100011111010110001000001010010"
    print("chiffrementLFSR : OK")
except :
    print("chiffrementLFSR : ERREUR")

Définir une fonction dechiffrementLFSR(c, k, coeff) qui retourne le clair de c moyennant la clé k.

# réponse

# test

try :
    assert dechiffrementLFSR("101001110111100101000101111111000011101001100011111010110001000001010010",[1,0,0,1],[0,2,3]) == "50ansGyYv"
    print("chiffrementLFSR : OK")
except :
    print("chiffrementLFSR : ERREUR")