M4202C_S - Statistique inférentielle
TP 2 - TCL
TP 2 - TCL
# importation des modules
import numpy as np
import numpy.random as npr
import scipy.stats as sps
import matplotlib.pyplot as plt
Remarque :
- Pour calculer les lois de probabilité (pmf ou pdf) et les fonctions de répartition (cdf), on utilisera scipy.stats (sps)
- Pour simuler des réalisations de variable aléatoire, on préfèrera numpy.random (npr)
Approcher une loi théorique (continue) par sa loi empirique¶
# loi théorique
x = np.linspace(-4, 4, 1000)
yTh = sps.norm.pdf(x)
plt.plot(x, yTh, 'r', label='Loi théorique')
# loi empirique
N = int(1e4)
nbCl = int(N**(1/3))
yEmp = npr.randn(N)
plt.hist(yEmp, bins=nbCl, normed=1, edgecolor='black', label='Loi empirique')
plt.legend(loc='best')
plt.show()
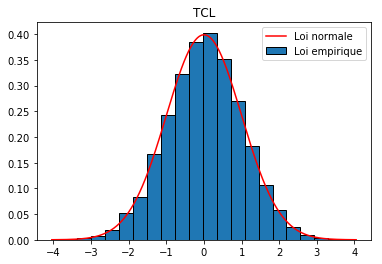
Théorème Central Limite¶
Nous savons maintenant (LFGN) que la moyenne empirique (pour $n$ assez grand) est "proche" de la moyenne théorique, mais comment se distribue-t-elle ?
Autrement dit, si l'on calcule plusieurs moyennes empiriques (pour un même $n$ assez grand), comment se répartissent-elles autour de la moyenne théorique ?
C'est le Théorème Central Limite (TCL) qui répond à cette question.
Théorème (TCL) :
Soit $X_i$ des v.a. indépendantes et de même loi (éventuellement inconnue) d'espérance $m$ et d'écart-type $\sigma$.
Alors, la moyenne empirique centrée réduite converge (en loi) vers la gaussienne centrée réduite :
$$\displaystyle\frac{\bar X_n-m}{\frac{\sigma}{\sqrt{n}}}\xrightarrow[n\to +\infty]{\mathcal L}\mathcal N(0,1)$$
En pratique, on considère que la loi de la moyenne empirique centrée-réduite est proche de la loi normale centrée-réduite.
Ecrire un script permettant d'illustrer ce théorème de la manière suivante, par exemple avec les $X_i$ de loi uniforme sur [0,1[.
# Réponse
Ecrire un script permettant d'illustrer le résultat suivant (p 15 du cours) : $$W=\displaystyle\frac{\bar X_n-m}{\frac{S^*}{\sqrt{n}}}\xrightarrow[n\to +\infty]{\mathcal L}\mathcal N(0,1)$$ Cette convergence en loi de la fonction (asymptotiquement) pivotale $W$ est le point de départ de la construction de l'intervalle de confiance (asymptotique) de la moyenne d'une variable aléatoire, non supposée gaussienne, lorsque l'écart-type est inconnu.
# Réponse