R3.08 - Probabilités
TP - Simulation probabiliste

A. Ridard

# importation des modules
import numpy as np
import numpy.random as npr
import scipy.stats as sps
import matplotlib.pyplot as plt

Remarque :

Pour calculer les lois de probabilité (pmf ou pdf) et les fonctions de répartition (cdf), on utilisera scipy.stats (sps)
Pour générer des tableaux de nombres aléatoires, on utilisera numpy.random (npr)

Lois usuelles finies : le point de vue théorique¶

Dans cette partie, nous allons représenter graphiquement les trois lois usuelles finies vues en cours.

Loi uniforme (sps.randint) sur $\{1,...,6\}$¶

fig, (ax1, ax2) = plt.subplots(1, 2)
plt.tight_layout(rect = [0, 0, 1, 0.85])
plt.suptitle('Loi uniforme sur $\{1,...,6\}$', fontsize=16)

ax1.set_title('Loi de probabilité')
ax1.set_ylim(-0.05, 1)
a = 1
b = 6
x = np.arange(a,b+1)
y = sps.randint.pmf(x, a, b+1)
ax1.stem(x, y)

ax2.set_title('Fonction de répartition')
x = np.linspace(-1, b+1, int(1e3))
y = sps.randint.cdf(x, a, b+1)
ax2.plot(x, y)

plt.show()

Loi de Bernoulli (sps.bernoulli) de paramètre $p = 0.3$¶

# Réponse

Loi binomiale (sps.binom) de paramètres $n = 20$ et $p = 0.3$¶

# Réponse

Lois usuelles finies : le point de vue empirique¶

Dans cette partie, nous allons effectuer nos premières simulations pour approcher les espérances vues en cours.

Utilisation des générateurs fournis par numpy.random (npr)¶

Pour chacune des lois suivantes :

Simuler 100 réalisations à l'aide du générateur adapté

Calculer la moyenne de ces 100 valeurs

Comparer cette moyenne empirique avec la moyenne théorique (espérance) vue en cours

Loi uniforme (npr.randint) sur $\{1,...,6\}$

# Réponse

Loi de Bernoulli (npr.binomial) de paramètre $p = 0.3$

# Réponse

Loi binomiale (npr.binomial) de paramètres $n = 20$ et $p = 0.3$

# Réponse

Définition de nos propres générateurs à partir de celui de la loi uniforme sur [0,1[ (npr.rand)¶

Loi uniforme sur $\{1,...,6\}$

A l'aide de npr.rand, définir une fonction myRandint qui génère un tableau de nombres aléatoires (selon la loi considérée)

Simuler 100 réalisations à l'aide de ce générateur

Comparer la moyenne empirique avec la moyenne théorique

# Réponse

Loi de Bernoulli de paramètre $p = 0.3$

A l'aide de npr.rand, définir une fonction myBernoulli qui génère un tableau de nombres aléatoires (selon la loi considérée)

Simuler 100 réalisations à l'aide de ce générateur

Comparer la moyenne empirique avec la moyenne théorique

# Réponse

Loi binomiale de paramètres $n = 20$ et $p = 0.3$

A l'aide de myBernoulli, définir une fonction myBinomial qui génère un tableau de nombres aléatoires (selon la loi considérée)

Simuler 100 réalisations à l'aide de ce générateur

Comparer la moyenne empirique avec la moyenne théorique

# Réponse

Remarque : on peut en fait simuler toutes les lois usuelles, même les lois continues, à l'aide de la seule loi uniforme sur [0,1[ !

Loi Forte des Grands Nombres¶

Nous avons observé, pour trois lois usuelles finies, que la moyenne empirique (pour 100 réalisations) était proche de la moyenne théorique.
En fait, ce résultat se généralise au travers du théorème de la Loi Forte des Grands Nombres (LFGN).

Théorème (LFGN) :

Soit $X_i$ des v.a. indépendantes et de même loi (éventuellement inconnue) d'espérance $m$.
Alors, la moyenne empirique converge (presque sûrement) vers la moyenne théorique : $$\bar X_n=\displaystyle\frac{1}{n}\sum_{i=1}^{n}X_i\xrightarrow[n\to+\infty]{(p.s.)}m$$

En pratique, on considère que la moyenne empirique (pour $n$ assez grand) est proche de la moyenne théorique

Ecrire un script permettant d'illustrer ce théorème de la manière suivante, par exemple avec les $X_i$ de loi uniforme sur [0,1[.

# Réponse

Remarque : si les $X_i\sim \mathcal B(p)$, alors la LFGN légitime l'approximation d'une probabilité par une fréquence empirique !

Justifier cette remarque

Réponse :

Applications de la LFGN¶

Résoudre un problème probabiliste par la simulation¶

Résoudre par simulation le problème de Monty Hall (cf. cours), autrement dit :

Simuler un grand nombre de "parties" (disons 100) avec les deux stratégies possibles.
Pour chacune des stratégies, on notera 1 si la partie est gagnée et 0 sinon

Calculer alors, pour chacune des stratégies, la fréquence empirique des parties gagnées.
Souvenez-vous, elle doit être proche de $\frac{2}{3}$ lorsque le joueur décide de changer d'avis, et proche de $\frac{1}{3}$ sinon.

Approcher une loi théorique par sa loi empirique¶

Dans le cas discret

# paramètres de la binomiale
n, p = 20, 0.3 

# loi théorique
x = np.arange(n+1)
yTh = sps.binom.pmf(x, n, p)
plt.stem(x, yTh, 'r', label='Loi théorique')

# loi empirique
N = int(1e4)
yEmp = npr.binomial(n, p ,N)
plt.hist(yEmp, bins=n+1, normed=1, range=(-0.5,n+0.5), rwidth=0.4, edgecolor='black', color='white', label='Loi empirique')

plt.legend()
plt.show()

Ecrire un script permettant de vérifier vos fonctions myRandint, myBernoulli et myBinomial.

# Réponse

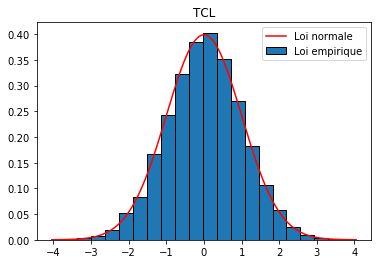
Dans le cas continu

# loi théorique
x = np.linspace(-4, 4, 1000)
yTh = sps.norm.pdf(x)
plt.plot(x, yTh, 'r', label='Loi théorique')

# loi empirique
N = int(1e4)
nbCl = int(N**(1/3))
yEmp = npr.randn(N)
plt.hist(yEmp, bins=nbCl, normed=1, edgecolor='black', label='Loi empirique')

plt.legend(loc='best')
plt.show()

Théorème Central Limite¶

Nous savons maintenant (LFGN) que la moyenne empirique (pour $n$ assez grand) est "proche" de la moyenne théorique, mais comment se distribue-t-elle ?
Autrement dit, si l'on calcule plusieurs moyennes empiriques (pour un même $n$ assez grand), comment se répartissent-elles autour de la moyenne théorique ?
C'est le Théorème Central Limite (TCL) qui répond à cette question.

Théorème (TCL) :

Soit $X_i$ des v.a. indépendantes et de même loi (éventuellement inconnue) d'espérance $m$ et d'écart-type $\sigma$.
Alors, la moyenne empirique centrée réduite converge (en loi) vers la gaussienne centrée réduite : $$\displaystyle\frac{\bar X_n-m}{\frac{\sigma}{\sqrt{n}}}\xrightarrow[n\to +\infty]{\mathcal L}\mathcal N(0,1)$$

En pratique, on considère que la loi de la moyenne empirique centrée-réduite est proche de la loi normale centrée-réduite.