TP3 - Génération d'une clef aléatoire
Registres à décalage à rétroaction linéaire (LFSR)
Registres à décalage à rétroaction linéaire (LFSR)
Certains exemples et textes de ce TP sont tirés de Exercices et Problèmes de cryptographie de Damien Vergnaud, 3ème édition ainsi que de Codes et Cryptologie de Christine Bachoc.
Ce TP traite d'un des aspects de la cryptographie symétrique moderne (post 1950) : la génération d'une clef binaire "aléatoire" pour le chiffrement d'un message, lui aussi binaire, selon le principe du masque jetable.
import numpy as np
import datetime as dt
1 - Messages en binaire et masque jetable¶
Avec l'arrivée des ordinateurs et du binaire, les messages sont d'abord convertis en suites de $0$ et de $1$ avant d'être transmis. Nous travaillerons donc maintenant non plus sur l'ensemble $\mathbb{Z}/26\mathbb{Z}$ mais sur $\mathbb{Z}/2\mathbb{Z}$ qui est un ensemble composé de deux valeurs $0$ et $1$.
Voici deux fonctions qui vous seront (certainement) utiles dans la suite du TP :
stringToBinaryconvertit une chaine de caractère en une suite binaire.binaryToStringpermet de changer une suite binaire en chaine de caractère.
def stringToBinary(msg):
msg_bin = ""
for i in bytearray(msg, encoding ='ascii') :
msg_bin = msg_bin + format(i, '08b')
return msg_bin
def binaryToString(binary):
msg = ""
for i in range(0, len(binary), 8):
byte_int = int(binary[i:i+8], 2)
byte_char = chr(byte_int)
msg = msg + byte_char
return msg
print("En binaire :", stringToBinary("message en clair"))
print("En ascii :",binaryToString(stringToBinary("message en clair")))
Le masque jetable, aussi appelé "chiffrement de Vernam", repose sur le principe du "ou exclusif" (xor, noté $\oplus$, opérateur ^ en python) bit à bit entre le message binaire à chiffrer et la clef de chiffrement (de même longueur).
Voici la table de vérité du "ou exclusif" : $$ 0 \oplus 0 = 0 $$ $$ 1 \oplus 1 = 0 $$ $$ 1 \oplus 0 = 1 $$ $$ 0 \oplus 1 = 1 $$
Ainsi, étant donné une clef k de longueur n (donc $k \in (\mathbb{Z}/2\mathbb{Z})^n$)
\begin{align*} E_k \colon (\mathbb{Z}/2\mathbb{Z})^n &\to (\mathbb{Z}/2\mathbb{Z})^n\\ m &\mapsto c = m \oplus k \end{align*}Par exemple, avec $m = 1100 1100$ et $k = 1010 1011$, on aura $c = 0110 0111$ (Vérifiez par vous même !)
Le masque jetable garantit la sécurité des messages à condition qu'une clef ne serve qu'au chiffrement d'un seul message (d'où le "jetable" du nom) sinon, la cryptanalyse devient possible.
Question 1 (masque jetable/Chiffrement de Vernam) : Définir une fonction
chiffrementVernam(msgBinaire, clef)qui étant donné un message en clair binairemsgBinaire, et une suite binaireclefde même longueur que le message retourne le message chiffré correspondant.
def chiffrementVernam(msgBinaire, clef):
return "TODO"
try:
assert chiffrementVernam(stringToBinary("vernam"),"110011001100110011001100110011001100110011001100") == "101110101010100110111110101000101010110110100001"
print("chiffrementVernam : OK")
except:
print("chiffrementVernam : ERREUR")
Le déchiffrement s'opère en executant la même opération : $m = c \oplus k$
Question 2 (déchiffrement) : Le démontrer.
TODO
Question 3 (déchiffrement) : Quel clair (en ascii) représente le chiffré "1010001010101101101010011011111010111000" codé avec la clef "1100110011001100110011001100110011001100" ? Ecrire le bout de code permettant de le déchiffrer.
print("TODO")
2 - Registre à décalage à rétroaction linéaire¶
En pratique, il existe deux inconvénients majeurs au principe du chiffrement par masque jetable :
- Les clefs doivent faire la même longueur que le message à chiffrer. Transmettre des clefs aussi longues est un problème en soi.
- Pour assurer la sécurité des messages, il faut que la clef soit choisie aléatoirement. Or, nous ne savons pas comment produire du vrai aléa.
Les registres à décalage à rétroaction linéaire ou LFSR (pour linear feedback shift register) permettent de pallier partiellement ces deux inconvénients en générant une suite binaire proche de l'aléatoire véritable à partir de quelques bits appelés graine. Il suffit donc de transmettre la graine ainsi que la fonction interne du LFSR, et non plus la suite entière, au recepteur du message pour qu'il puisse déchiffrer le message.
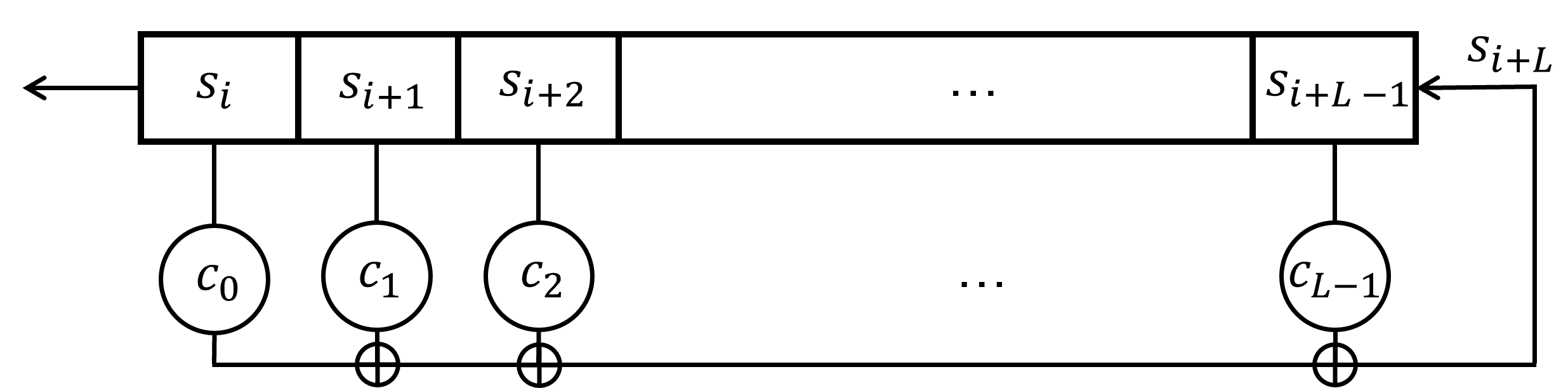
Un LFSR binaire de longueur $L$ est composé :
- d'un registre à décalage contenant une suite de $L$ bits ($s_i$, $s_{i+1}$, ..., $s_{i+L−1}$) décrivant l'état interne du registre.
- d'une fonction de rétroaction linéaire permettant de calculer la valeur du bit suivant à insérer dans le registre.
A chaque top d'horloge, le bit $s_i$ constitue la sortie du registre, et les autres sont décalés ; le nouveau bit $s_{i+L}$, placé dans la cellule rendue libre du registre, est donné par une fonction linéaire : $s_{i+L} = c_0s_{i} \oplus c_1s_{i+1} \oplus ... \oplus c_{L−1}s_{i+L-1}$ où les coefficients $c_i$ sont binaires.
On appelle suite chiffrante la concaténation des sorties du registre. C'est cette suite qui servira ensuite de clef de chiffrement.
On peut représenter ce LFSR de la manière suivante :
Ci-dessous un exemple de LFSR de longueur $L = 4$ initialisé avec la graine $1001$ à $t_0$:
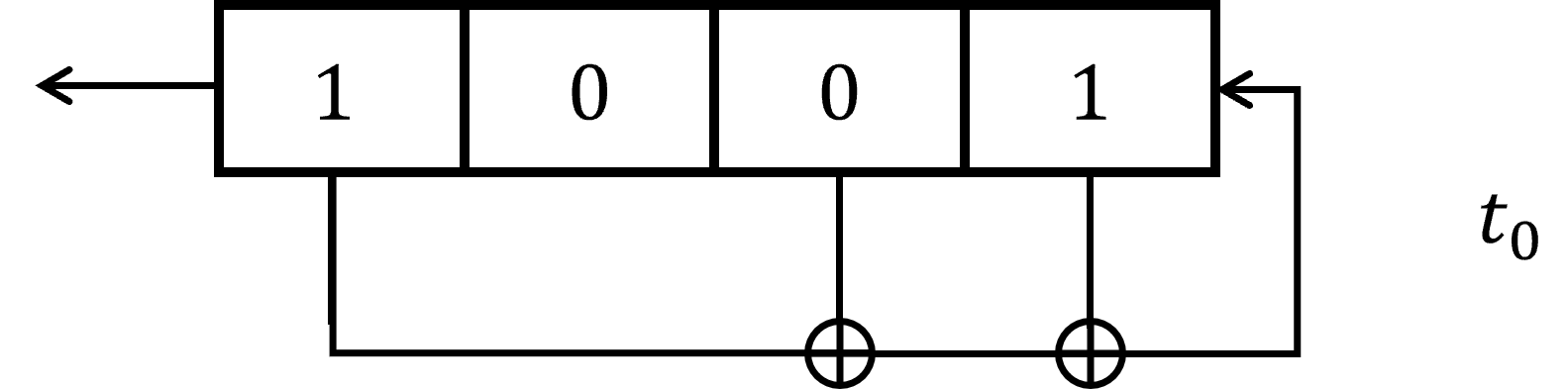
Les coefficients de la fonction de rétroaction sont : $c_0 = 1, c_1 = 0, c_2 = 1, c_3 = 1$.
Le bit inséré à droite est donc calculé grace à la formule : $s_{i+4} = s_{i} \oplus s_{i+2} \oplus s_{i+3}$.
Nous avons déroulé les 2 premières itérations ($t_1$ et $t_2$) du registre. A l'étape $t_1$, la sortie est le bit situé le plus à gauche du registre (de valeur $1$). A l'étape $t_2$, c'est le bit $0$ qui sort permettant de créer la suite chiffrante $10$ en considérant la sortie de l'étape précédente.
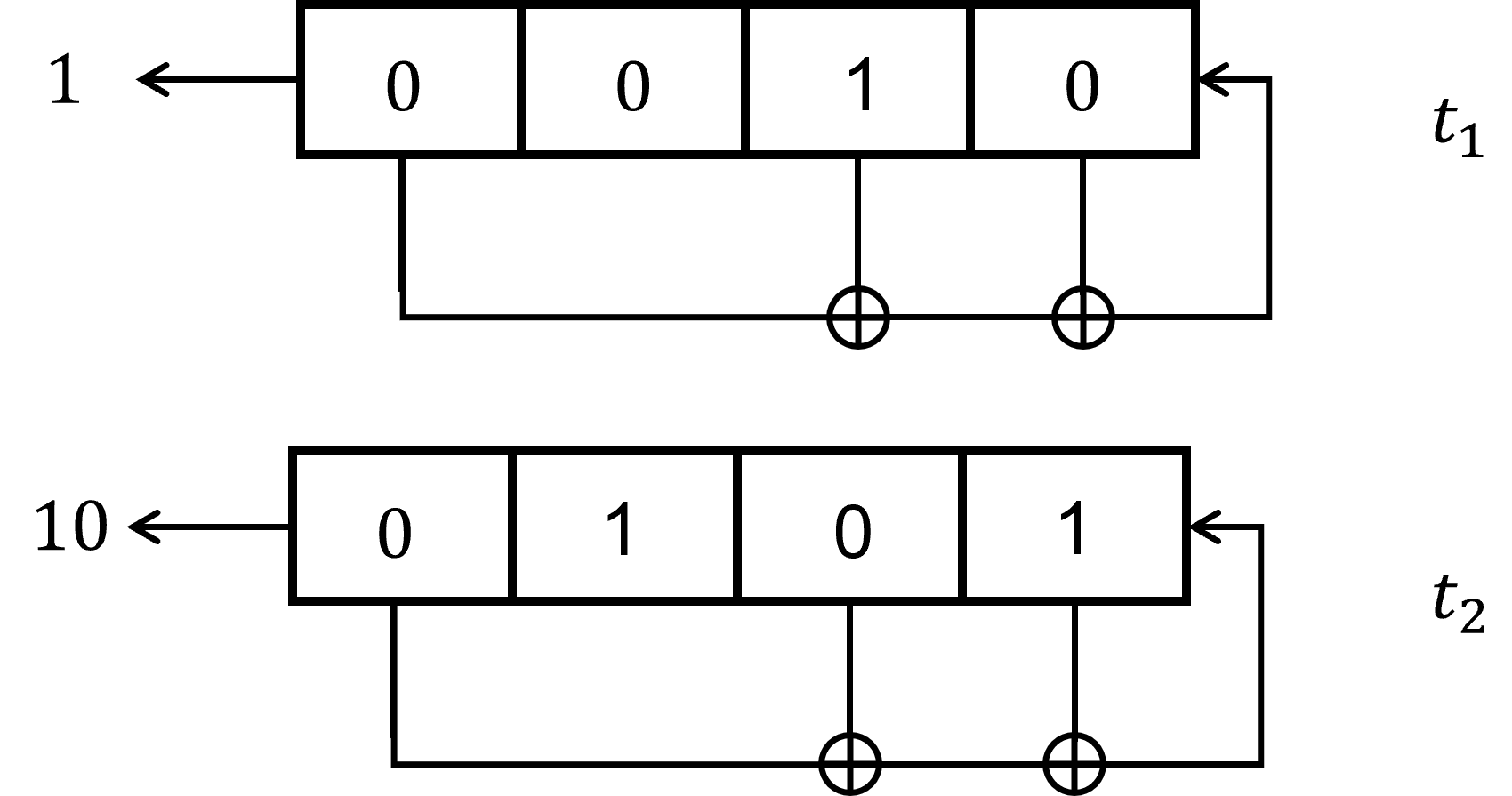
Question 4 (suite chiffrante) : Quelle sera la suite chiffrante à $t_{14}$ ? Que remarquez vous ?
TODO
Question 5 (registre à décalage) : Ecrire une fonction
etatSuivant(etat,coeff)qui prend une liste binaire correspondant à l'état interne du registre ainsi qu'une liste des coefficients de rétroaction non nuls (i.e. indices des cases sur lesquelles faire le xor) et renvoie l'état suivant du registre et le bit de sortie.
def etatSuivant(etat,coeff):
return "TODO"
try:
assert etatSuivant([1,0,0,1],[0,2,3]) == ([0, 0, 1, 0],1) #Exemple précédent t1
assert etatSuivant(etatSuivant([1,0,0,1],[0,2,3])[0],[0,2,3]) == ([0, 1, 0, 1],0) #Exemple précédent t2
print("etatSuivant : OK")
except:
print("etatSuivant : ERREUR")
Question 6 (suite chiffrante) : Ecrire une fonction
suite_LSFR(graine,coeff,n)qui prend en entrée une liste binaire correspondant à la graine du registre, une liste des coefficients de rétroaction non nuls et la longueur souhaitée de la suite chiffrante et qui renvoie la suite chiffrante bianire sous forme d'une chaine de caractère.
def suite_LFSR(graine,coeff,n):
return "TODO"
try:
assert suite_LFSR([1,0,0,1],[0,2,3],14) == "10010111001011"
print("suite_LFSR : OK")
except:
print("suite_LFSR : ERREUR")
La fonction suivante permet de générer une graine d'une taille précisée en paramètre. N'hésitez pas à l'utiliser pour tester vos méthodes.
def generation_reg_graine(taille):
"""
Génération d'une graine de taille "taille" basée sur l'heure
"""
### Transformation de la date en une chaine de caractères
date = str(dt.datetime.now())
#print(date)
### Transformation de la fin de la chaine en un entier compris entre 0 et 255 pour pouvoir le représenter avec 8 bits
init_entier = int(date[-4:]) % 2**taille # j'ai choisi de prendre les 4 derniers caractères arbitrairement
### Représentation de l'entier sur un octet
init_bin = bin(init_entier)[2:] # on retire le 0b qui permet de préciser qu'il s'agit d'un nombre binaire
while len(init_bin) < taille :
init_bin = '0' + init_bin # on rajoute des 0 pour que le nombre produit soit composé de taille bits. (padding)
#print(init_bin)
### Transformation de la chaine des bits en une liste
init_reg = [int(x) for x in init_bin]
return init_reg
init_reg = generation_reg_graine(8)
print('La graine est égale à :', init_reg,'\n')
Question 7 (Chiffrement par LFSR) : Ecrire une fonction
chiffrementLFSR(msgAscii, graine,coeff)qui déroule l'ensemble du processus de chiffrement par masque jetable généré par LSFR et retourne la version binaire du message chiffré.
def chiffrementLFSR(msgAscii, graine,coeff):
return "TODO"
try:
assert chiffrementLFSR("naert",[1,0,0,1],[0,2,3]) == "1111100101001111001110011100101100000110"
print("chiffrementLFSR : OK")
except:
print("chiffrementLFSR : ERREUR")
Question 8 (Déchiffrement par LFSR) : Ecrire une fonction
dechiffrementLFSR(msgChiffBinary, graine,coeff)qui déroule l'ensemble du processus de déchiffrement et retourne la version ascii du message en clair.
def dechiffrementLFSR(msgChiffBinary, graine,coeff):
return "TODO"
try:
assert dechiffrementLFSR("1111100101001111001110011100101100000110",[1,0,0,1],[0,2,3]) == "naert"
print("chiffrementLFSR : OK")
except:
print("chiffrementLFSR : ERREUR")
Activité 1 : Chiffrer un message à l'aide d'une clef générée par un LFSR de taille 8 et envoyez le message chiffré, la graine et les coefficients de votre LFSR à votre voisin(e) pour qu'il/elle le déchiffre.
Ouverture cryptanalyse : Les LFSR sont susceptibles d'être cryptanalysés en utilisant un pivot de Gauss. Vous pouvez vous référer à "Exercices et Problèmes de cryptographie" de Damien Vergnaud pour plus d'informations.
3 - Générateur à signal d'arrêt¶
En pratique, la suite chiffrante produite par un unique LFSR n'est pas assez complexe pour servir de clef de chiffrement. Nous avons vu notamment à la question 4 que les LFSR pouvait produire des suites chiffrantes périodiques donc loin d'une suite réellement aléatoire. En réalité, toute suite chiffrante produite par un unique LSFR est ultimement périodique.
Définitions :
Soit une suite $s = (s_0,s_1,s_2...)$ avec pour tout $i \in \mathbb{N}$, $s_i \in \mathbb{Z}/2\mathbb{Z}$
On dit que $s$ est périodique de période T si $s_i = s_{i+T}$ pour tout $i \ge 0$
On dit qu'une suite $s$ est ultimement périodique de période T si $s_i = s_{i+T}$ pour tout $i$ supérieur ou égal à un certain rang appelé $i_0$. Ainsi, une suite périodique est ultimement périodique ($i_0 = 0$) mais la réciproque est fausse.
Question 9 (BONUS) : Ecrire une fonction
periode(graine,coeff)qui donne la plus petite période de la suite générée par le générateur défini pargraineetcoeffainsi queTrues'il s'agit d'une suite périodique etFalsesi elle est ultimement périodique avec $i_0 \gt 0$ .
def periode(graine,coeff):
return "TODO"
print("Suite périodique : ", suite_LFSR([1,0,0,1],[0,2,3],14))
print("Suite ultimement périodique (mais non périodique) : ",suite_LFSR([1,0,1,1],[1,2,3],14))
try:
assert periode([1,0,0,1],[0,2,3]) == (7,True)
assert periode([1,0,1,1],[1,2,3]) == (4,False)
print("periode : OK")
except:
print("periode : ERREUR")
Pour générer des suites chiffrantes utilisables dans un système cryptographique, les LFSR sont utilisés comme briques de base de système plus complexes : plusieurs LFSR peuvent être combinés pour atteindre la complexité souhaitée. Dans ce TP, nous étudierons un exemple d'un tel générateur : le générateur à signal d'arrêt.
Le générateur à signal d'arrêt (GSA) est un exemple de registre à décalage irrégulier (1984). Il utilise la sortie d'un premier LFSR $R_1$ pour contrôler l'horloge d'un second LFSR $R_2$. Plus précisément, $R_1$ est un LSFR "normal" dont le décalage est commandé par un signal d'horloge (en orange sur l'image ci-dessous) mais $R_2$ ne change d'état à l'instant $t$ que si la sortie de $R_1$ (en vert) est égale à 1 à l'instant $t-1$, autrement dit si la sortie de $R_1$ est égale à 0 à l'instant $t-1$, alors $R_2$ n'est pas décalé et le bit de sortie à l'instant $t$ est donc toujours égal au bit de sortie à l'instant $t-1$.
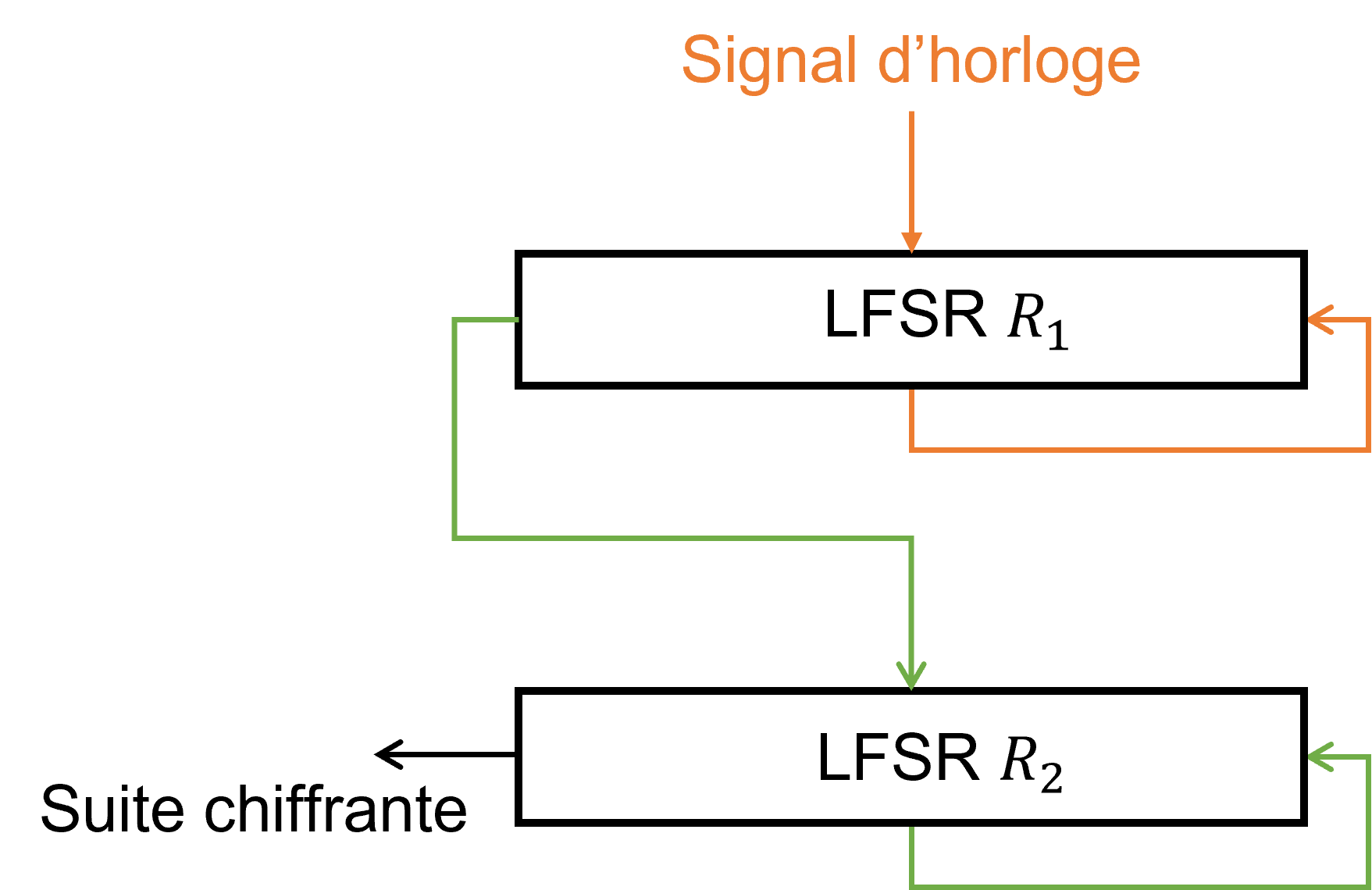
Question 10 (générateur à signal d'arret) : Ecrire une fonction
suite_gsa(graineR1,coeffR1, graineR2, coeffR2, n)qui renvoie la suite chiffrante binaire de longueurngénérée par un générateur à signal d'arret composé de R1 et R2.
def suite_gsa(graineR1,coeffR1, graineR2, coeffR2, n) :
return "TODO"
print("10 premiers termes de la suite chiffrante : ", suite_gsa([1,0,1,0,1,1,0,0],[0, 3, 5],[1,0,1,0,1,0,1,0], [0, 2, 5, 6],10))
try:
assert suite_gsa([1,0,1,0,1,1,0,0],[0, 3, 5],[1,0,1,0,1,0,1,0], [0, 2, 5, 6],10) == "1001101111"
print("suite_gsa : OK")
except:
print("suite_gsa : ERREUR")
Activité 2 : Chiffrer un message à l'aide d'une clef générée par un générateur à signal d'arrêt et envoyez le message chiffré à votre voisin(e) (avec éventuellement d'autres informations pour qu'il/elle puisse le déchiffrer).